Az összekötő folyami csatornától a soliton internetig

John Scott Russell

   1834 augusztusában John Scott Russell skót mérnöknek rendkívüli élményben volt része, amikor egy alkalommal  kilovagolt az Edinburgh közelében lévő Union Canal ( Edinburgh-Glasgow- összekötő csatorna) partjára. Emlékirataiban a következőképpen írt erről: „ ...figyeltem egy hajót, ahogyan a szűk csatorna mentén egy lovas fogat meglehetősen sebesen vontatta, majd hirtelen megállt; de nem így azonban az általa mozgásban tartott víz, amely először vadul örvénylett a hajó orra körül, majd azt hirtelen elhagyva, nagy sebességgel hömpölygött tova, s közben felvette egy simára lekerekített, jól körülhatárolt hullám alakját, amely a csatornában látszólag változatlan formában és nem csökkenő sebességgel haladt tovább. Lóháton követtem hát ezt a hullámot, majd megelőztem, közben még mindig változatlan, 8-9 mérföldnyi sebességgel haladt, s eredeti alakját, kb. 30 láb1 hosszúság és másfél láb magasságú formáját megtartotta. Minekutána az egészet 1-2 mérföldnyi távon követtem, magassága kezdett lassan csökkeni, s a csatorna egyik kanyarjában szem elől tévesztettem.”

   Russell tapasztalt hajómérnök lévén azonnal tudta, milyen rendkívüli jelenséget figyelhetett meg. Nem is tudott szabadulni tőle életének hátralévő, majdnem fél évszázada alatt. Hogy miben állt a megfigyelés rendkívülisége, alig szükséges magyarázni, hiszen mindenki tudja saját tapasztalatából, hogy mindennemű, általunk létrehozott vízhullám belátható időn belül szertefoszlik, legyen az egy tóban vagy a fürdőkádban. A hullám széttöredezését nevezi a fizika diszperziónak. A Russell által megfigyelt hullám rendkívülisége éppen a diszperzió hiányából adódik, s az ilyen hullámot a tudomány szolitonnak (a lat. solitariusból = egyes, egyedüli, magányos) nevezi, mely fogalom ma, éppen a káoszelmélet részeként, korunk forradalmi felismeréseként járja a tudomány berkeit, amiről azt mondja G. Binning fizikai Nobel-díjas, hogy kihatása a természettudományokban a kvantummechanikáéhoz lesz hasonló. (Ami után kezdetben ugyancsak kevés érdeklődés mutatkozott; így pl. Heisenberg előadásait 1927-ben, Lipcsében csupán három hallgatónak tartotta.)

   A hullámok alapformája a szinusz-hullám: minden hullám belőle vezethető le, vagy belőle építhető fel, ez ugyanis a legegyszerűbb forma, amelyet egy hullám vagy rezgés felvehet, és valamennyi egységes jellemvonása a frekvencia. Ha több szinusz-hullámot fűzünk össze, akkor mindenféle komplikált forma nyerhető. Ezen az alapelven működik különben a zenei szintetizátor, amellyel bármilyen kívánt hang reprodukálható.

   Szinusz-hullámok akkor szenvednek diszperziót, ha egymástól függetlenül fordulnak elő egy lineáris rendszerben. Ha azonban nem-lineáris rendszerben fordulnak elő, ahol kölcsönös kapcsolatok érvényesülnek (az ún. feed-back: visszacsatolás), ami lehet pozitív vagy negatív, amelyek révén, ha a feltételek adva vannak, az egyes hullámok egymáshoz kapcsolódnak, nem engedvén őket szabadon, hogy széttöredezzenek. Bizonyos szempontból a turbulencia ellentétének felel meg.

   A szinusz-hullámok egymáshoz kapcsolhatóságának feltétele továbbá egy bizonyos kritikus érték, ami nyilván nem mindig és minden nem-lineáris rendszerben, és tetszés szerint fordul elő. A szolitonok létrejöttének fenti módjából az is adódik, hogy határterületek terméke. Ha a kezdeti energia túl nagy, akkor turbulenciába torkollik, ha túl kevés, akkor elhal, mivel nem éri el a kritikus szükséges értéket; szoliton tehát a kettő közötti határterületen alakul(hat) csak ki.

   Russell persze mindezt nem tudhatta, de a kertjében felállított kísérleti berendezésében tetszés szerint tudott előállítani szolitonokat, amelyeket ő transzlációs hullámnak nevezett. Megállapította azt is, hogy a hullámok magassága és tovaterjedési sebessége összefüggést mutat, továbbá hogy a berendezés mélysége is szerepet játszik létrejöttükben. Így arra is rájött, hogy a megfigyelt hullám nem jött volna létre, ha a csatorna mélyebb lett volna. Russellnak sikerült a szoliton terjedési elve alapján értelmeznie, miért hallható egy bizonyos távolságból először az ágyúdörej, s csak utána a vezényszó: a dörej ugyanis szoliton-hullámként gyorsabban terjed, mint a hang. A szoliton elve alapján kiszámította (helyesen) az atmoszféra vastagságát is.

   Russellt haláláig foglalkoztatta az általa megfigyelt hullám természete és rejtélye. Biztosan érezhette azt is, hogy ennek jelentősége messze túlterjed a Union Canal határain. Halála (1882) után fia adta ki a Transzlációs hullámok c. könyvét. Sajnos, kortársai nem sokat tudtak vele kezdeni, sőt, egyik kritikusa szerint Russellt megszállottsága „rendkívüli és feneketlen spekulációkra csábította”.

   Tíz évvel Russell halála után, D. J. Korteweg és C. de Vries holland matematikusok egy nem-lineáris egyenletet írtak le (ma KdV-egyenlet), amely a Russell hullámait egyik megoldásként tartalmazza. Ennek ellenére visszhang nélküli kuriózum maradt továbbra is.

   A KdV-egyenlet megerősítette Russell számításait, s különösen a két szoliton találkozásakor történteket, amit számítógépes szimulációk teljes egészében bizonyítottak. Miről van hát itt szó?

   Ha két szoliton találkozik, éspedig úgy, hogy egy vékony és magas szoliton utolér egy vastagabbat és alacsonyabbat, akkor rövid időre a kettő egyesül, egybeolvadtnak látszik, majd roppant érdekes dolog történik: a pillanatnyilag egyetlen hullámnak tűnő szoliton újból kétfelé válik, éspedig a két szoliton pontos eredeti formájában. Ennek alapján merült fel a gondolat, hogy a nem-lineáris kapcsolatok egyféle „emlékezést” is magukban rejtenek, hiszen itt a másodszor keletkezett hullámok „emlékeztek” eredeti formájukra.

A KdV-egyenlet leírja és matematikailag magyarázza a folyamok torkolatában megfigyelt, már említett jelenséget: a Severnnél észleltek magyarázata abban rejlik, hogy itt az apály és dagály közötti vízszintkülönbség 6 m-t tesz ki, ami miatt hatalmas víztömeg tódul be a folyó torkolatába és áramlik visszafelé, s ezt az állandóan emelkedő mederfenék (emelkedik, mivel visszafelé folyás történik) szolitonná modulálja. Hasonló történik az Amazonas torkolatában is.

   A nyílt óceánokon szoliton után kutatni csak műholdak segítségével lehetett, amelyek minden kétséget kizáróan bizonyították a 100-200 km (!) hullámhosszú, de alig pár centiméter vagy deciméter (!) magasságú, egymást követő hullámok létét, amelyek tovahaladási sebessége csekély, a hajók, ill. hajósok észre sem veszik, hiszen ők hozzá vannak szokva nagy, valódi szélvihar okozta, drámai hullámverésekhez. Nos, ezeket a nyílt tengeri szolitonokat, amelyeket cunami-nak2 (szökőár) nevezünk, földrengés vagy tenger alatti vulkánkitörés váltja ki, és hatalmas víztömegeket tartanak mozgásban! A nagy baj akkor kezdődik, amikor az ilyen hullámok elérik a partot, és a sekély vízben a nem-lineáris kölcsönhatások eredményeképpen az addigi extrém hullámhossz megrövidül, és szélsőségesen megnő a hullám magassága, ugyanakkor felgyorsul az addigi lassú sebesség, aminek az eredménye borzalmas: egy 10 cm magas hullámból keletkezik egy 30 m magas hullám, amilyen minden valószínűség szerint a leírt, 1775-ben Lisszabont pusztító lehetett. Hasonló lehetett a Japánban 1702-ben több mint 100 000 ember életét kioltó „nagy hullám” – majd 1883-ban a Krakatau vulkán kitörését követő szökőár.

    A levegőben észlelhető szolitonra példaként említettük az ágyúdörgéssel kapcsolatosakat. 1951. június 19-én azonban sikerült Kansas államban egy rendkívüli légnyomás-hullám szolitonját megfigyelni, kb. 200 km hosszú volt, 2 km magasságban vonult kb. 20 km/h sebességgel, s több száz km-t tett meg; nyilván csak nem-lineáris kölcsönhatások tarthatták életben ilyen sokáig. Nem érdektelen megemlíteni, hogy ma a fizikusok a Jupiter felületén észlelhető vörös foltokat is atmoszferikus szolitonnak tartják, s így érthető nagy stabilitásuk és azon körülmény is, hogy miért nem észlelték őket a csillagászok 1713 és 1831 között.

   A tenger hullámairól is azt gondoltuk, hogy teljesen véletlenszerűek mind formájuk, mind eloszlásuk szerint, azaz a tenger felülete nem egyéb volna, mint maga a rendetlenség képmása, ami teljesen ad hoc, véletlen jön létre. Mivel azonban a nem-linearitás mindenütt érvényesül, feltételezni kell, hogy a tenger felületének bonyolult rajzolata a rendnek egy igen szubtilis formáját képviseli, ami akár szubminimális erőbehatás folytán kaotikussá válhat3. Yuan és Lake szavaival élve: a tenger felülete rendkívül modulált, olyannyira, hogy minden előző állapotának formáját magában hordozza. A nagy hullámot nem véletlenül ható, örvénylő és sodró erők eredményeinek láthatjuk, hanem úgy tekinthetjük, hogy benne az óceán emlékezése egy szoliton formájában kulminál, ill. ölt formát.

   A szolitonokkal kapcsolatosan érdemes megemlíteni egy kérdést, amely már Michael Faradayt is foglalkoztatta: Miért ég a gyertya folyamatosan és nem fellobbanásokkal? Faraday összegzése szerint „a gyertya lángjában benne foglaltatik minden fizika és kémia.”

   A gyertya csodája abban áll, hogy az intenzív égési folyamatok ellenére többé-kevésbé folytonos erősségű és formájú lángot és fényt nyerünk. Miért? Ha Russell szolitonja egy érzékeny nem-lineáris egyensúlyi állapotot jelent a diszperzió területén, akkor a gyertyaláng jelenti ugyanezt a diffúzió területén. Ahhoz ugyanis, hogy a gyertya égjen, energiának kell az égés színhelyére, a lángba beáramolnia, éspedig olyan ütemben, ahogyan hő és fény származik és adódik le a környezetbe. Ehhez a viasz megolvad és kapillaritás révén folyamatosan felszáll a kanócon a lángba; ugyanakkor feltétlenül szükséges, hogy kellő mennyiségű oxigén is diffundáljon be a lángba. A gyertya szolitonja jelenti a kifelé és befelé irányuló diffúziós áramlások közötti egyensúlyi állapotot, ami a természet egyik csodája.

   A szolitonok olyan nagy amplitudójú nemlineáris hullámok, melyek szemben a kis amplitúdójú lineáris hullámokkal, megtartják koherens alakjukat. A fizikai kutatás szempontjából a szolitonok egyik külön érdekessége, hogy hullámcsomag jellegűek, s részecsketulajdonsággal is rendelkeznek (például ütközés után visszanyerik eredeti alakjukat). Rétegzett folyadékokban a szolitonok kétfélék lehetnek. A belső szolitonok a közeg belsejében, a különböző sűrűségű rétegek határán terjednek. Ezeket a természetben keltheti például az árapály-hatás az óceánok felső, melegebb vízrétegét az alsótól elválasztó ún. termoklin zónában, vagy egy gyorsan mozgó hideg front az előtte tolt meleg levegőben. (Felszíni szolitonok a szabad felszínen jönnek létre. Ezekre egy félelmetes példa a vizes közegben a földrengések által keltett "tsunamik", amelyek több ezer km-t is haladnak az óceánban, mielőtt a sekély partokon megtörve pusztító energiájuk felszabadul.)

A szolitonoknak  rendkívüli jelentősége van a neurobiológiában is.

A szoliton-elmélet előtt ún. „bioenergetikai krízisről” beszéltek, mivel érthetetlen volt, hogyan lehet energiát szállítani hosszú molekulákon keresztül. Ti. lineáris viszonyokat tételezve fel, energia csak úgy tud továbbterjedni, hogy a célban kevesebb érkezik meg a kiindulási értéknél, disszipáció miatt. Legelőször az orosz Davidov tette fel a kérdést: spirális fehérjemolekulák esetében energia szállításakor vajon nem nem-lineáris kölcsönhatások érvényesülnek-e? Davidov úgy gondolta, hogy egy bizonyos küszöb alatti energia a spirál rezgése miatt szállítás közben fokozatosan szétszóródik az egész molekulában. Küszöb feletti mennyiségű energia esetében azonban a nem-linearitás képes kell hogy legyen a diszpergáló-diffúziós erők kiegyenlítésére, ami által lehetségesnek kell lennie, hogy energia-pakettek a spirálon több mint 1000 m/s. sebességgel szaladjanak végig, veszteség nélkül. Ekképpen lenne lehetséges a sejten belüli energia szállítása.

   Ma azonban azt is tudjuk, hogy az idegszálakon a jelzések ugyancsak szoliton formájában terjednek tova. Az idáig vezető út azonban nem érdektelen. Az idegvezetés úttörő kutatói anynyit tudtak, hogy az egész folyamat alapjául bioelektromos történések szolgálnak. Aztán a 19. század végén, a 20. elején úgy gondolták ugyanis, hogy az idegingerület az éppen akkor feltalált telefon és távíró elve alapján működne, ami érthetőnek is látszott, habár már akkor megmutatkozott az elmélet gyenge pontja, nevezetesen, hogy amíg a drótokban az elektromos impulzus a fény terjedési sebességével halad tova, addig az idegszálakban csak kb. 10 méterrel másodpercenként.

   Hogy és miért? Az ún. bioenergetikai krízis is mutatta azt a zsákutcát, amelyben a kutatás megfeneklett. Aztán a második világháború során, éppen hadi jelentősége és fontossága miatt, a kutatók nagy haladást értek el az elektronika területén, ami végül is azt az alapot jelentette, amely lehetővé tette a nyitott kérdések megválaszolását.

   A. L. Hodgkin angol kutató a háború alatt radarkutatással foglalkozott, majd a háború után visszatérve cambridge-i laboratóriumába, 1945-ben nekilátott vizsgálni, hogyan terjednek tova az impulzusok a tintahal óriási idegrostjaiban. E vizsgálatokra a tintahal ideális alany. Hodgkinnak az első megállapítása volt, hogy az idegszálban az ingerület tovaterjedése semmi esetre sem a telefonhoz hasonlóan történik, hanem konstans sebességgel és formaváltozás nélkül haladó impulzus-pakettek formájában. Továbbá, hogy egy ilyen pakett csak akkor jöhet létre, ha egy kritikus energetikai küszöböt elér vagy meghalad. Ezekért a vizsgálatokért kapott Hodgkin, A. F. Huxleyvel és J. C. Ecclesszel együtt orvosi Nobel-díjat, 1963-ban.

Ezt az impulzus-csomagot nevezzük ma szolitonnak, és ennek tulajdonítható, hogy az impulzus, ill. információ konstans sebességgel és disszipáció, tehát veszteség nélkül szállítható.

Rendkívüli jelentőségű felismerés.

  

  Egy biológiai neuron vázlat

 Egy mesterséges neuron vázlata

1.A biológiai neurális hálózat a gócok csatlakozása, vagy funkcionálisan összefüggő neuronok, a periférikus idegrendszerben, vagy a központi idegrendszerben. A neurális tudományok területén a leggyakrabban az idegrendszer egy csoportjának azonosítják, mely laboratóriumi analizálásra alkalmas.

2.A mesterséges neurális hálózat, egy biológiai indíttatású gép/program, ami a biológiai neurális hálózat néhány tulajdonságát modellezi. Az alkalmazások többsége technikai jellegű, és nem kognitív modell. Fontos megjegyezni, hogy a mesterséges neurális hálók nem csak a biológia, hanem más tudományterületek (matematika, fizika, pszichológia) eredményeit is felhasználják.

A neurális hálózatok alapelve, hogy a számolásokat egymással összekapcsolt kis feldolgozóegységek, mesterséges neuronok (a továbbiakban: neuronok) végzik. A számítások során fontos szerepet játszik a neuronok közötti kapcsolatrendszer, ezért a neurális hálókat konnekciós hálózatoknak, a velük foglalkozó szakembereket pedig konnekcionistáknak is nevezik.

A neurális hálózat egyszerű egységekből áll, abban az értelemben, hogy belső állapotai leírhatók számokkal, ezek az aktivációs értékek. Mindegyik egység generál egy aktiválási értéktől függő kimeneti értéket. Az egységek csatlakoznak egymáshoz, mindegyik csatlakozás tartalmaz egy egyéni súlyt (szintén számokkal leírva). Minden egység kiküldi a kimeneti értékét az összes többi egységnek, amelyekkel kimenő kapcsolatban vannak. Ezen kapcsolatok miatt az egység kimenete hatással van a másik egység aktivációjára. A kapcsolat bemeneti oldalán álló egység fogadja az értékéket, és azok súlyozásával kiszámolja az aktivációs értékét (összeszorozza a bemeneti jelet a hozzá tartozó bemenet súlyával, és veszi ezek összegét) A kimenetet az aktivációtól függően az aktivációs függvény határozza meg. (pl az egység kimenetet generál –„tüzel”- ha az aktivizáció egy határérték felett van) A hálózat legtöbb esetben a csatlakozások súlyának módosításával tanul. A súlymódosítás során az ún. hibafüggvény eredményét veszi figyelembe. A hibafüggvény értékét sokféle módon lehet kiszámítani, a legegyszerűbb eset, amikor a kimeneti értékből kivonja a helyes kimeneti értéket.

Fontos megjegyezni, hogy a neuronok bár számításokat végeznek ugyan, de mégsem processzorok! A fő különbség a kettő között az, hogy amíg a processzorokat programozzák (szekvenciális utasítássorozatot adnak meg neki), addig a neuronokat tanítják (a súlymátrix értékeinek beállításával)!

 Szolitonok mint információhordozók.

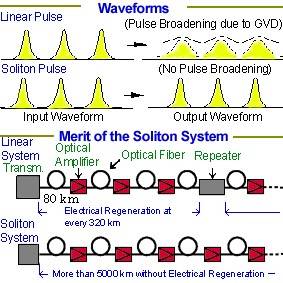
 A szolitonok rendkívül érdekes, és meglehetősen stabil hullámformák, amelyek viszonylag hosszú ideig (nagy távolságon) stabilan megőrzik alakjuk és sebességük. A solitonok viselkedésének kutatása napjainkban is népszerű kutatási téma. Jelentőségük ott van, hogy jelenleg a távközlésben használt jelekre igaz, hogy Fourier komponenseik terjedési sebessége függ a közegtől amiben terjednek. Ez azt eredményezi, hogy a küldött jelek egy idő után elkezdenek torzulni, ahogy az egyes komponensek lemaradoznak. Egy idő után a kapott jel értelmezhetetlenné válik A szoliton típusú jelek jellegzetessége, hogy a "lemaradozó" elnyúló komponensek kioltják egymást, emiatt noha a jel -mint a hagyományos- fokozatosan gyengül, ám alakja sokkal hosszabb távon stabil marad. Ezáltal szoliton rendszerű átvitellel távolabbra lehetne jelet küldeni.

Oldal: Hogyan működik a HuPont.hu weboldalszerkesztő és honlap?
SOLITON A MAGÁNNYOS HULLÁM - © 2008 - 2024 - soliton.hupont.hu

Ingyen weblap készítés, korlátlan tárhely és képfeltöltés, saját honlap, ingyen weblap.

ÁSZF | Adatvédelmi Nyilatkozat